Maschinelles Lernen (ML) wird oft anhand von Metriken wie Accuracy, Precision, Recall, F1-Score etc. bewertet. Doch wie vertrauenswürdig sind diese einzelnen Werte wirklich? Diese Metriken geben nur einen Teil der Realität wieder und können ein falsches Gefühl der Sicherheit vermitteln. Besonders in sicherheitskritischen Bereichen kann das gefährlich werden. Das Fraunhofer IKS arbeitet an einem formalen Framework, mit dem sich die Unsicherheit quantifizieren lässt. Damit werden Restrisiken »berechenbarer«.
1. August 2024
© iStock/iiievgeniy
Maschinelles Lernen (ML) wird immer häufiger in sicherheitskritischen Anwendungen eingesetzt, zum Beispiel bei der Bilderkennung für autonomes Fahren. Doch wie sicher sind ML-Modelle wirklich? Grob gesagt gibt es zwei Hauptansätze, an diese Frage heranzugehen. Die ML-Community entwickelt Metriken und Techniken, um die Qualität eines Modells hinsichtlich unterschiedlicher Kriterien zu bewerten. Die Safety-Community hingegen analysiert die Ursachen von Fehlern, um sicherzustellen, dass das Risiko akzeptabel bleibt. Das Fraunhofer-Institut für Kognitive Systeme IKS arbeitet daran, beide Welten besser miteinander zu verbinden.
Eine der Publikationen des Fraunhofer IKS in diesem Kontext beleuchtet die Herausforderung der ML-Sicherheitsbewertung vor dem Hintergrund der Unsicherheit [1]. Dort wird argumentiert, dass zur Sicherheitsbewertung die Identifikation und Reduktion verschiedener Unsicherheitsfaktoren notwendig ist. Diese Unsicherheit wird in drei Schichten unterteilt: (1) Modell, (2) Daten und (3) Umgebung (Eingaberaum + vom Modell zu lösende Aufgabe), wie unten als Zwiebelmodell dargestellt:
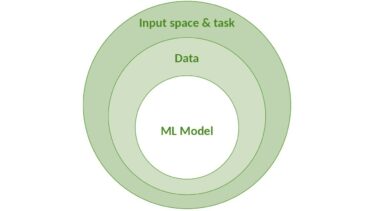
© Fraunhofer IKS
Das Zwiebelmodell stellt Unsicherheit in drei Schichten dar.
Stellen wir uns vor, dass ein neuronales Netz zur Klassifikation eine Accuracy von 99 Prozent bei der Erkennung von Fußgängern erreicht. Klingt erstmal nicht schlecht. Aber was ist mit dem restlichen Prozent? Und wie verlässlich sind diese 99 Prozent, wenn man z.B. die Kalibrierung des Modells, die Menge, Qualität und Abdeckung der Trainings- und Testdaten oder die Qualität der Umgebungsbeschreibung in Betracht zieht? Wenn auch nur eine dieser Komponenten schwach ist, kann die alleinige Aussagekraft dieser Performanzmetrik mit hoher Unsicherheit behaftet sein.
Um wirklich überzeugend zu sein, muss ein Sicherheitsargument eine ganzheitliche Perspektive bieten und Evidenzen aus allen drei oben genannten Unsicherheitsschichten beinhalten. Jedoch sollte man diese Evidenzen nicht isoliert betrachten. Forscherinnen und Forscher des Fraunhofer IKS arbeiten deshalb mit Prof. Simon Burton von der University of York an einem formalen Framework, das dabei hilft, Evidenzen formal zu modellieren und zu kombinieren, um damit die Gesamtunsicherheit zu ermitteln [2]. Dazu wird Subjective Logic [3] verwendet, ein formaler Ansatz, der probabilistische Logik mit Unsicherheit und Subjektivität kombiniert. Erreicht werden soll Folgendes:
Betrachten wir als Beispiel das Problem der ML-basierten Verkehrszeichen-erkennung. Diese kann z.B. als Teil eines Autobahnpiloten eingesetzt werden, um die automatische Steuerung des Fahrzeugs je nach Situation zu aktivieren/deaktivieren. Zentrale Komponente ist ein neuronales Netz zur Klassifikation, das auf einem entsprechenden Datensatz trainiert wurde. Ziel ist es, sicherzustellen, dass das Netz so wenige Baustellenschilder wie möglich übersieht.
Da es hier primär um die Vermeidung von False Negatives geht, d.h. um Fälle, in denen das Modell ein Baustellenschild übersieht oder fälschlicherweise nicht erkennt, liegt der Fokus auf Recall (auch Sensitivität oder True Positive Rate genannt) als unsere primäre Metrik. Angenommen, eine Analyse der True Positives und False Negatives des neuronalen Netzes ergibt für die Klasse der Baustellenschilder folgende Werte:
Hieraus lässt sich der Recall des Modells wie folgt berechnen: TP/(TP+FN) = 98%. Das sieht erstmal gut aus, die entscheidende Frage ist jedoch, wie vertrauenswürdig dieser Wert wirklich ist. Hierfür sind versteckte Einflussfaktoren zu berücksichtigen, die sich wiederum in die drei oben erwähnten Schichten aufteilen lassen: Modell, Daten und Umgebung.
Hier kommt jetzt der Ansatz des Fraunhofer IKS ins Spiel. Die Recall-Messung wird als »Subjective Opinion« modelliert, d.h. als mathematisches Konstrukt, das das subjektive Vertrauen in die Messung vor dem Hintergrund der verwendeten Datenmenge ausdrückt: Diese formalisierte Opinion können wir als Wahrscheinlichkeitsmessung visualisieren, die beschreibt, wie wahrscheinlich der von uns gemessene Recall-Wert ist:
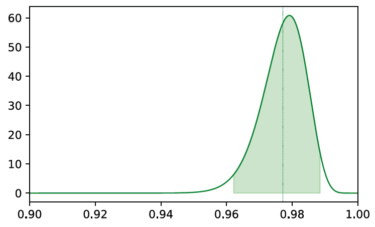
© Fraunhofer IKS
Die Grafik zeigt die Beta-Wahrscheinlichkeitsverteilung des gemessenen Recall-Werts. Der Erwartungswert der Verteilung ist als vertikale grüne Linie dargestellt, der grün hinterlegte Bereich zeigt das 95% Glaubwürdigkeitsintervall.
Sichtbar wird, dass wir dem ursprünglich gemessenen Wert von 98 Prozent nicht komplett vertrauen können: Die Streuung der Verteilung deutet auf eine gewisse Unsicherheit hin, die sich in einem Erwartungswert (grüne vertikale Linie) niederschlägt, der etwas unter den ursprünglich gemessenen 98 Prozent liegt. Diese Unsicherheit resultiert zunächst lediglich aus der begrenzten Menge an Datenpunkten (480), die der Messung zugrunde lagen.
Wie erfolgt jetzt die Annäherung an den tatsächlichen Wert? Hierzu können wir zunächst den Bereich ermitteln, in dem der tatsächliche Wert mit einer gewissen Wahrscheinlichkeit (z.B. 95 Prozent) liegt (in obiger Grafik grün hinterlegt). Um mit der Recall-Messung auf der sicheren Seite zu sein, sollte diese also nach unten korrigiert und beispielsweise den unteren Rand des grün hinterlegten Bereichs als konservative Schätzung verwendet werden. Damit kommt ein korrigierter Recall-Wert von 96 Prozent, zwei Prozentpunkte unter den ursprünglich gemessenen 98 Prozent. Und hier gingen bisher lediglich die Größe des Testdatensatzes in die Betrachtung ein, nicht aber andere Einflussfaktoren!
Als nächstes wird die Kalibrierung des Modells gemessen, die ihrerseits wiederum die Korrektheit der True Positives und False Negatives beeinflusst, auf Basis derer wir den Recall berechnet haben. Hierfür kommt der Brier-Score [4] zum Einsatz. Der gemessene Brier-Score für die Klasse der Baustellenschilder liegt bei 0.004, was auf eine sehr gute Kalibrierung hinweist. Auch diese Messung können wir wieder als Subjective Opinion formalisieren und als Wahrscheinlichkeitsverteilung visualisieren:
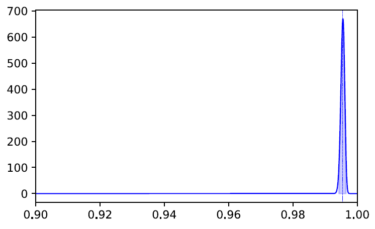
Die Grafik zeigt die Beta-Wahrscheinlichkeitsverteilung des gemessenen Brier-Scores. Die wesentlich geringere Streuung im Vergleich zur vorherigen Abbildung zeigt, dass die Messung mit weniger Unsicherheit behaftet ist.
Interessant wird es jetzt, wenn beide Messungen kombiniert werden und somit unseren Belief in die ursprüngliche Recall-Messung unter Berücksichtigung der Kalibrierung ausdrücken:
Die Grafik veranschaulicht die Kombination der beiden vorherigen Messungen (links und Mitte), sowie den Vergleich der resultierenden kombinierten Messung mit dem ursprünglichen Recall-Wert hinsichtlich der durch das Glaubwürdigkeitsintervall repräsentierten Unsicherheit (rechts).
Im rechten Graph ist zu sehen, dass sich die Unsicherheit in der ursprünglichen Recall-Messung (grün hinterlegt) deutlich erhöht, wenn wir zusätzlich unser Wissen über die Kalibrierung des Modells hinzufügen. Der rot hinterlegte Bereich beschreibt die Unsicherheit der kombinierten Messung. Aus Safety-Perspektive sollte durch die Berücksichtigung der Kalibrierung also der konservative Schätzwert für Recall erneut reduziert werden – von zuvor 96 Prozent um einen Punkt auf ca. 95 Prozent. Der ursprünglich gemessene Wert von 98 Prozent fällt also mittlerweile um drei Prozentpunkte geringer aus!
Dieser Blogbeitrag basiert auf einem Paper von Benjamin Herd und Simon Burton mit dem Titel: »Can you trust your ML metrics? Using Subjective Logic to determine the true contribution of ML metrics for safety«.
Der Prozess hört hier natürlich nicht auf und weitere Einflussfaktoren aus Modell-, Daten- und Umgebungsebene können (und sollten) in die Betrachtung einfließen. Die kombinierte Modellierung einzelner (vormals isolierter) Metriken ermöglicht es, eine ganzheitlichere Sicht auf die Performanz eines Modells zu bekommen und die Gesamtunsicherheit greifbarer zu machen. Der beschriebene Ansatz des Fraunhofer IKS kann somit beispielsweise einen wichtigen Beitrag zur Ermittlung der Konfidenz in ein Sicherheitsargument leisten, in dem auf strukturierte Art und Weise belegt werden soll, wie unterschiedlichste Metriken als Evidenzen fungieren, um in ihrer Gesamtheit die Erfüllung eines übergeordneten Sicherheitsziels zu zeigen.
[1] Burton, Herd (2023): Addressing uncertainty in the safety assurance of machine-learning. Frontiers in Computer Science, Volume 5
[2] Herd, Burton (2024): Can you trust your ML metrics? Using Subjective Logic to determine the true contribution of ML metrics for safety. Proceedings of the 39th ACM/SIGAPP Symposium on Applied Computing (SAC ’24)
[3] Jøsang, Audun (2016): Subjective Logic: a formalism for reasoning under uncertainty. Artificial Intelligence: foundations, theory and algorithms. Springer International Publishing Switzerland.
[4] Brier (1950). Verification of forecasts expressed in terms of probability. Monthly weather review 78, 1 (1950), 1–3.
Diese Arbeit wurde im Rahmen des Projekts ML4Safety durch Fraunhofer-interne Programme gefördert.
