Tiefe neuronale Netze (Deep Neural Networks, DNNs) haben ihr Potenzial unter Beweis gestellt. Dies gilt vor allem für ihre Verwendung im Labor. Ihre Leistung beim Einsatz in der Praxis lässt allerdings zu wünschen übrig. Ein wesentliches Problem ist die Schätzung der Unsicherheit (uncertainty). Im Folgenden werden die Methoden näher betrachtet, die dieser Herausforderung gerecht werden.
8. Oktober 2020
© iStock.com/gremlin
Das Potenzial tiefer neuronaler Netze (Deep Neural Networks, DNNs) ist ein Thema, das die Wissenschaft in den letzten Jahren stark beschäftigt hat. Der Hype um DNNs erscheint angesichts der beeindruckenden Ergebnisse, die mit diesen Netzen im Bereich Computer Vision erzielt wurden, durchaus begründet. Forscher haben die Fortschritte bei den Architekturen mit verschiedenen Bildklassifizierungs-, Objekterkennungs- und Segmentierungsdatensätzen als Benchmarks verfolgt und gemessen. Ihre Erkenntnisse bestätigen, dass DNN-basierte Modelle ihr Potenzial im Labor entfalten. Die Leistung beim Einsatz in der Praxis ist bisher jedoch weniger beeindruckend – insbesondere bei sicherheitskritischen Systemen.
Diese Modelle, die für die optimale Arbeit mit einem bestimmten Datensatz trainiert sind, neigen dazu, allzu selbstsichere Vorhersagen zu treffen. Sie sind häufig nicht zur »Out of Distribution«-Erkennung in der Lage. Hinzu kommt, dass die meisten Rahmenkonzepte derzeit nicht in der Lage sind, Unsicherheit auszudrücken, weshalb Softmax-Konfidenzwerte heute die Basismethode für die Bestimmung der Genauigkeit von Netzwerkergebnissen sind.
Bayes’sche neuronale Netze (BNNs) – eine statistisch modifizierte Version von DNNs – verwenden keine festen Gewichtungen wie Standard-DNNs, sondern drücken die Unsicherheit inhärent durch Erlernen einer Verteilung über die Gewichtungen aus. Das birgt jedoch einen Nachteil: Dieses Bewusstsein geht mit einem erheblichen Rechenaufwand einher.
Stichprobenbasierte Methoden wie Monte Carlo Dropout und Deep Ensembles nähern sich BNNs an, indem sie die Varianz über mehrere Vorhersagen für dieselbe Eingabe berechnen. Dies erfordert mehrere Vorwärtsdurchläufe, was die Inferenzzeit erhöht.
Bei anderen Methoden wird die Unsicherheitsabschätzung in das Modell eingebettet. So kann beispielsweise ein Modell mit einer in seine Verlustfunktion integrierten Kullback-Leibler-Divergenz (KL-Divergenz) sowohl die Bounding-Box-Koordinaten als auch die Varianzen vorhersagen.
Conference Paper, 2020
Unsicherheitsschätzungen helfen nicht nur bei der Erkennung falsch-positiver Detektionen. Es liegen Hinweise darauf vor, dass sie auch ein besserer Indikator als Konfidenzwerte dafür sind, wie gut die Box-Vorhersagen mit den tatsächlichen Objekten in einem Bild übereinstimmen.
Zur Überprüfung dieser Hypothese führten Forscher ein Experiment mit dem KITTY-Datensatz (Karlsruher Institut für Technologie, KIT) durch. Sie berechneten hierfür die IoU (Intersection over Union) jeder vorhergesagten Bounding Box mit der gegebenen Ground Truth, also der tatsächlichen Kartographie der echten visualisierten 3D Struktur, für konfidenzbasierte und varianzbasierte Modelle. Bei diesem Experiment wurden Efficientdet-D0-Standardmodelle mit Efficientdet-D0-Modellen verglichen, die mit der KL-modifizierten Verlustfunktion trainiert wurden, was es diesen Modellen ermöglicht, sowohl Varianzen als auch Box-Koordinaten vorherzusagen.
Die in den nachstehenden Abbildungen gezeigten Ergebnisse bestätigen, dass Varianzen tatsächlich ein besserer Indikator für die räumliche Genauigkeit von Detektionen sind. Die Korrelation ist ebenfalls stärker (wobei zu beachten ist, dass eine höhere Varianz mit einer größeren räumlichen Unsicherheit einhergeht, was die negativen Detektionen erklärt). Die Korrelation für Konfidenzen ist immer noch gegeben, aber schwächer ausgeprägt. Es ist zu beachten, dass schlechte Schätzungen bei den Konfidenzen häufiger vorkommen, wie aus den Streudiagrammen (a) und (b) hervorgeht. Die Punkte konvergieren in der oberen rechten bzw. der oberen linken Ecke in dichteren Gruppen, was auf gute Schätzungen bei hohen IoU-Werten hinweist. Die Verteilung der Konfidenzen für die übrigen Punkte ist jedoch nahezu gleichmäßig. Andererseits erwiesen sich die Varianzen mit einer größeren Konzentration rund um das Polynom erster Ordnung, die zu den Stichproben passt, als genauer. Das Histogramm in (d) stützt diese Schlussfolgerung mit seinem steilen Abfall der IoU für Detektionen mit hoher Varianz.
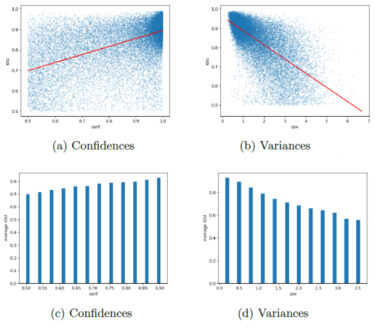
© Fraunhofer IKS
Korrelation zwischen Intersection over Union (IoU) und Vertraulichkeiten/Varianzen.
Wir wissen, dass die Beurteilung der Unsicherheit für eine sichere Entscheidungsfindung wichtig ist. Zudem wissen wir jetzt, dass die Varianzen die räumliche Genauigkeit der erkannten Bounding Boxes besser ausdrücken. Wie beurteilen wir dann Unsicherheitsschätzungen?
Die bei der Objekterkennung am häufigsten verwendete Metrik mAP (Mean Average Precision) berücksichtigt die Unsicherheit nicht. Sie stuft einfach jede Erkennung mit einer IoU oberhalb eines bestimmten Schwellenwerts als True Positive ein. Liegt dieser Schwellenwert bei 0,5, setzt die mAP eine positive Erkennung bei gerade einmal 0,5 IoU mit einer perfekten Übereinstimmung mit der Ground Truth gleich.
Zur Lösung dieses Problems haben Forscher ein Evaluierungsmaß entwickelt – Probability-based Detection Quality (PDQ). PDQ verwendet eine kategoriale Verteilung über alle Klassenlabels für die gegebene Klassifizierungsaufgabe und eine Wahrscheinlichkeitskarte (Probability Map) mit einem Satz von Pixeln für die Objektlokalisierung. Diese Metrik besteht aus zwei Indizes, der Labelqualität und der räumlichen Qualität. Die Labelqualität wird durch die Wahrscheinlichkeit definiert, die der Detektor dem wahren Label zuordnet. Die räumliche Qualität summiert die logarithmischen Wahrscheinlichkeiten, die der Detektor den Pixeln eines Ground-Truth-Segments zuordnet. Bei diesem Index werden Detektionen stark abgewertet, wenn der Detektor einem Pixel, das nicht mit der Ground Truth übereinstimmt, eine hohe Wahrscheinlichkeit zuordnet.
DNNs haben ihr Potenzial unter Beweis gestellt. Die Herausforderung besteht nun darin, dieses Potenzial auf sichere Weise zu nutzen, um diese Netze in kritische Systeme zu integrieren. Die Forschungsgemeinschaft hat sich bereits auf die Suche nach neuen Entwicklungen im Bereich der künstlichen Intelligenz begeben und hat dabei Unsicherheit, Erklärbarkeit und Robustheit im Blick. Mit unsicherheitsbewussten Objektdetektoren und einer geeigneten Metrik für die Beurteilung von Unsicherheitsschätzungen ist sie nun umso besser dafür gerüstet, Fortschritte auf diesem Weg zu erzielen.
Dieses Vorhaben wurde durch das Bayerische Staatsministerium für Wirtschaft, Landesentwicklung und Energie im Rahmen des Projekts Unterstützung des thematischen Aufbaus des Instituts für Kognitive Systeme gefördert.
