Nächster Artikel
Unsicherheitsbestimmung, Teil 2
Der KI das Zweifeln beibringen: So geht‘s
Bei autonomen Systemen oder in der Medizintechnik ist es nötig, die Unsicherheit von Verfahren des Machine Learning (ML) zuverlässig zu bestimmen. Deswegen vergleichen wir vier State-of-the-art-Methoden für die Quantifizierung der Unsicherheit tiefer neuronaler Netze (Deep Neural Network, DNN) im Kontext sicherheitskritischer Systeme – damit die KI lernt, wann Zweifel angebracht sind.



© iStock.com/Palana997
(Sie haben Teil 1 noch nicht gelesen? Hier finden Sie den ersten Artikel: »Uncertainties, auf die man sich verlassen kann«)
Bei den Verfahren, die hier auf dem Prüfstand stehen, liegt der Fokus auf der Bildklassifizierung. Das bietet sich an, um die Zahl der möglichen Einflussfaktoren auf die Analysen möglichst gering zu halten. Die Aufgabe der DNNs ist dabei, für verschiedene Bilder die entsprechende Klasse, z.B. Fußgänger oder PKW, zu bestimmen.
Verfahren mit Sampling
Die erste und wohl bekannteste Methode, um die Unsicherheit bei DNNs zu bestimmen, heißt Monte-Carlo-Dropout. Voraussetzung dafür ist, dass das DNN, welches verwendet werden soll, mit der Regularisierungsmethode Dropout trainiert wurde. Dabei werden während des Trainings bei jedem Schritt einzelne Neuronen mit einer gewissen Wahrscheinlichkeit deaktiviert. Im Gegensatz zur klassischen Herangehensweise, bei der während der Vorhersage keine Neuronen inaktiv gesetzt werden. Beim Monte-Carlo-Dropout bekommt das DNN mehrmals dieselben Bilder zu sehen, jedoch mit verschiedenen deaktivierten Neuronen. Somit können die Ergebnisse der einzelnen Durchläufe kombiniert werden, sodass die tatsächliche Verteilung der Wahrscheinlichkeiten über die Klassen angenähert wird. Der Mittelwert und die Varianz dieser Verteilung dienen dann als Unsicherheitsmaß. Bei der üblichen Klassifizierung mit der Softmax-Funktion handelt es sich hingegen nur um eine Punktschätzung der Wahrscheinlichkeit. Diese kann nicht zur zuverlässigen Bestimmung der Unsicherheit verwendet werden und weist bei empirischen Analysen deutlich zu hohe Konfidenzen auf.
Dem Monte-Carlo-Dropout ähnelt die Methode namens Deep Ensembles. Der Kerngedanke dabei ist, dass dasselbe DNN auf denselben Daten, jedoch mit unterschiedlicher Initialisierung der Neuronengewichte trainiert wird, wodurch diese zu verschiedenen lokalen Minima konvergieren. Für die Vorhersage werden schließlich ein Ensemble aus den DNNs gebildet und die Einzelvorhersagen kombiniert. Das Resultat ist damit ebenfalls ein Mittelwert und eine Varianz über die verschiedenen Vorhersagen der einzelnen DNNs.
Verfahren ohne Sampling
Die beiden bisher genannten Methoden gehören zu den Sampling-based-Verfahren, benötigen also zur Bestimmung einer einzelnen, kombinierten Vorhersage mehrere Vorhersageschritte. Vor allem für leistungsschwächere eingebettete Systeme können diese Verfahren aus Performance-Gründen ungeeignet sein. Aus diesem Grund haben wir noch zwei weitere Methoden betrachtet, die mit nur jeweils einem Vorhersageschritt auskommen.
Das erste Verfahren ohne Sampling, Learned Confidence, lernt explizit die Konfidenz für eine Vorhersage auszugeben. Erreicht wird dies, indem ein Teil des Netzwerks die korrekte Klassifizierung der Eingabebilder lernt, wie es auch bei den anderen Methoden der Fall ist. Zusätzlich gibt es hier aber noch einen zweiten Teil, der darauf trainiert wird, eine möglichst genaue Aussage darüber zu treffen, wie sicher sich das Netzwerk bei der Klassifizierung ist.
Das Evidential Deep Learning hingegen bringt Ideen aus der Evidenztheorie in DNNs ein. Konkret werden hier, anstelle einer üblichen Klassifizierung mit Softmax, die Parameter einer Dirichlet-Verteilung gelernt, welche dann für die Vorhersage verwendet werden kann. Dies soll zu besser kalibrierten Wahrscheinlichkeiten zwischen den Klassen sowie einer Gesamtunsicherheit über die Vorhersage führen.
Autonome Systeme: Welches Verfahren überzeugt?
Die vorgestellten Methoden haben verschiedene Vor- und Nachteile und wurden teilweise auch schon hinsichtlich allgemeiner Eigenschaften verglichen. Welchen Mehrwert die Verfahren jedoch konkret bieten können, etwa im Kontext der Vier-plus-Eins-Sicherheitsarchitektur des Fraunhofer IKS, ist noch wenig erforscht und der Punkt, an dem wir mit unserer Arbeit ansetzen.
Wird die Unsicherheit mit in die Vorhersage eines DNN miteinbezogen, so gibt es bei der Auswertung neben der Dimension »richtig und falsch« nun zusätzlich »sicher und unsicher«. Ob ein DNN sicher oder unsicher ist, hängt von einem Schwellenwert ab. So kann etwa definiert werden, dass die Entscheidung eines DNN bei einem Unsicherheitswert unter 20 % als sicher und in den anderen Fällen als unsicher gilt. Insgesamt ergeben sich die folgenden vier Möglichkeiten für eine Entscheidung:
- sicher und richtig,
- sicher und falsch,
- unsicher und richtig,
- unsicher und falsch.
Für das Gesamtsystem hat die Einbeziehung der Unsicherheit zur Folge, dass weniger Fehler gemacht werden, da unsichere und falsche Vorhersagen herausgefiltert werden können. Jedoch werden auch unsichere, aber eigentlich richtige Vorhersagen verworfen, was eine Reduktion der Performance des Gesamtsystems zur Folge hat.
Neue Metriken mit Aussagekraft
Um diesen Trade-off greifbar zu machen haben wir zwei neue Metriken definiert: Die Remaining Error Rate (RER) und die Remaining Accuracy Rate (RAR). Bei beiden wird angenommen, dass unsichere Vorhersagen herausgefiltert werden. RER gibt an, wie viele Fehlvorhersagen, RAR wie viele korrekte Vorhersagen im Verhältnis zu allen Vorhersagen übrigbleiben.
Wird das Ganze über verschiedene Schwellenwerte für die Klassifizierung als sicher oder unsicher berechnet und visualisiert, so werden verschiedene Charakteristika der einzelnen Verfahren deutlich:
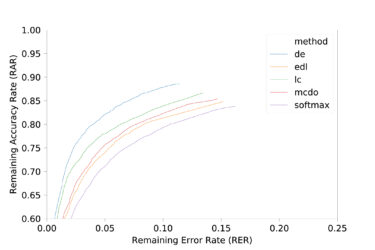
© Fraunhofer IKS
Remaining Accuracy Rate (RAR) und Remaining Error Rate (RER) auf dem CIFAR-10-Datensatz
Aus dem Graphen wird ersichtlich, dass eine starke Reduktion der Fehlerrate möglich ist, jedoch mit stellenweise sehr hohen Performanceeinbußen. Auch könnte der Schluss gezogen werden, dass, wenn die Rechenleistung verfügbar ist, Deep Ensembles verwendet werden sollten, andernfalls Learned Confidence. Bei anderen Datensätzen ist das Bild jedoch nicht mehr so eindeutig:
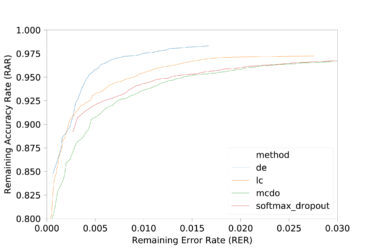
© Fraunhofer IKS
Remaining Accuracy Rate (RAR) und Remaining Error Rate (RER) auf dem German Traffic Sign Recognition Datensatz
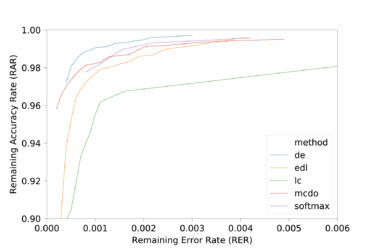
© Fraunhofer IKS
Remaining Accuracy Rate (RAR) und Remaining Error Rate (RER) auf dem MNIST-Datensatz
Auch bei Verwendung verschiedener Architekturen gibt es zwischen den Verfahren nochmals Unterschiede. Ebenso wenn man einen Distributional Shift zwischen Trainings- und Testdaten beachten muss. Es ist also nicht pauschal bestimmbar, welches Verfahren für welchen Anwendungsfall am besten geeignet ist und es müssen immer die spezifischen Vor- und Nachteile abgewogen werden. Deswegen unterstützt Sie das Fraunhofer IKS bei der Auswahl der richtigen KI-Methoden. Kontaktieren Sie dafür gerne bd@iks.fraunhofer.de.
Weitere Ergebnisse zum Vergleich der vier State-of-the-art-Methoden finden Sie in folgendem Paper:
Conference Paper, 2020
Benchmarking Uncertainty Estimation Methods for Deep Learning With Safety-Related Metrics
Publica.fraunhofer.deUncertainties, auf die man sich verlassen kann
Den ersten Teil dieser kleinen Blogserie zum Thema Unsicherheitsbestimmungen finden Sie hier: Uncertainties, auf die man sich verlassen kann


