Read next
Uncertainty Estimation in Object Detection – a mission-critical task
Deep Neural Networks (DNNs) have proven their potential. This applies above all to their use in the laboratory. Their performance in real-world applications leaves a lot to be desired. One major problem is the estimation of uncertainty. A closer look at methods that meet this challenge.



© iStock.com/gremlin
The promise of deep neural networks (DNN) has had the science community abuzz in recent years. DNNs’ claim to fame would seem well founded in view of the impressive results these networks have achieved in computer vision. Researchers have tracked and measured advances in the architectures using various image classification, object detection and segmentation datasets as benchmarks. Their findings confirm that DNN-based models deliver on that promise in the lab. However, their performance in real-world applications has been less impressive – particularly in safety-critical systems.
Trained to excel at working with a given dataset, these models tend to make overconfident predictions. They are frequently unable to spot out-of-distribution detections. What’s more, most frameworks today are unable to express uncertainty, which is why softmax confidence scores are today the baseline method for determining the accuracy of network outputs.
Object detection and uncertainty
Rather than using fixed weights in the way of standard DNNs, Bayesian neural networks (BNNs) – a statistically modified version of DNNs – inherently express uncertainty by learning a distribution over weights. There is a caveat, though – this awareness comes at the cost of considerable computational effort.
Sampling-based methods such as Monte Carlo Dropout and Deep Ensembles approximate BNNs by computing variance over multiple predictions for the same input. This requires multiple forward passes, which increases inference time.
Other methods embed uncertainty estimation into the model. For example, a model with Kullback-Leibler (KL) divergence integrated into its loss function can predict both bounding box coordinates and variances.
Conference Paper, 2020
Assessing Box Merging Strategies and Uncertainty Estimation Methods in Multimodel Object Detection
Publica.fraunhofer.deConfidence versus variance
Uncertainty estimates not only help spot false positive detections. Evidence suggests they are also better indicators than confidence scores of how well box predictions match the true objects in an image.
Researchers performed an experiment using the KITTY dataset (Karlsruher Institut für Technologie, KIT) to validate this hypothesis. To this end, they computed the intersection over union (IoU) of each predicted bounding box with the given ground truth for confidence-based and variance-based models. This experiment compared vanilla Efficientdet-D0 models to Efficientdet-D0 models trained using the KL-modified loss function, which enables these models to predict variances as well as box coordinates.
The results as shown in the figures below confirm that variances are indeed a better indicator of the spatial accuracy of detections. The correlation is also stronger (bearing in mind that higher variance translates to greater spatial uncertainty, which explains the negative detections). The correlation for confidences is still there, but weaker. Note that poor estimates are more frequent for confidences, as scatter plots (a) and (b) show. Points converge in denser groups at the top right and top left corners, respectively, indicating good estimates for high IoU values. However, the distribution of confidences for the remaining points is nearly uniform. On the other hand, variances proved more accurate, with a greater concentration around the first-order polynomial matching the samples. The histogram in (d) underpins this conclusion with its steep drop in the IoU for high variance detections.
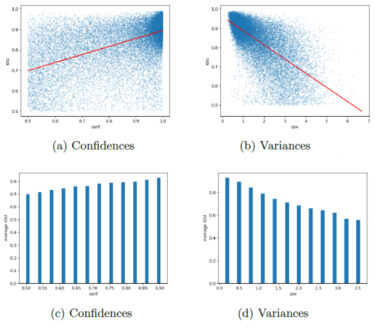
© Fraunhofer IKS
Correlation between intersection over union (IoU) and confidences/variances.
Evaluating uncertainty in object detection tasks
We know that assessing uncertainty matters to safer decision-making. And we now know that variances better express the spatial accuracy of detected bounding boxes. How, then, do we evaluate uncertainty estimates?
The most frequently used metric in object detection, mAP (mean average precision) fails to consider uncertainty. It simply deems every detection with an intersection over union above a certain threshold to be a true positive. If this threshold is 0.5, mAP equates a positive detection at just 0.5 of IoU with a perfect match for the ground truth.
Researchers have come up with an evaluation measure to resolve this issue – Probability-based Detection Quality (PDQ). PDQ uses a categorical distribution over all class labels for the given classification task and a probability map with a set of pixels for object localization. This metric consists of two indexes, label quality and spatial quality. Label quality is defined by the probability the detector assigns to the true label. Spatial quality sums the log probabilities the detector assigns to the pixels of a ground-truth segment. This index penalizes detections heavily when the detector assigns a high probability to a pixel that does not match the ground truth.
Expectations and prospects
DNNs have proven their potential. The challenge now is to how to safely tap this potential so as to integrate these networks into critical systems. The research community has already set out in pursuit of new advances in AI with uncertainty, explainability and robustness in mind. And with uncertainty-aware object detectors and a suitable metric to evaluate uncertainty estimates in their kitbags, they are all the better equipped to make strides down that road.
This activity is being funded by the Bavarian Ministry for Economic Affairs, Regional Development and Energy as part of a project to support the thematic development of the Institute for Cognitive Systems.



